1. DEFINITION
Given a function and a point in the domain, the derivative at that point is a way of encoding the small-scale behavior of the function near that point. In mathematical jargon, the derivative is a linear operator which inputs a function and outputs a second function.
The most common symbol for a derivative is an apostrophe-like mark called prime. Thus, the derivative of the function of f is f′, pronounced "f prime." For instance, if f(x) = x2 is the squaring function, then f′(x) = 2x is its derivative, the doubling function.
If a function is linear (that is, if the graph of the function is a straight line), then the function can be written as y = mx + b, where x is the independent variable, y is the dependent variable, b is the y-intercept, and:
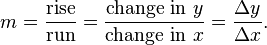 This gives an exact value for the slope of a straight line.
This gives an exact value for the slope of a straight line.
If the graph of the function is not a straight line, however, then the change in y divided by the change in x varies. Derivatives give an exact meaning to the notion of change in output with respect to change in input. To be concrete, let f be a function, and fix a point a in the domain of f. (a, f(a)) is a point on the graph of the function. If h is a number close to zero, then a + h is a number close to a. Therefore (a + h, f(a + h)) is close to (a, f(a)). The slope between these two points is
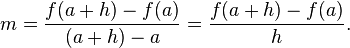 This expression is called a difference quotient.
This expression is called a difference quotient.
The derivative is defined by taking the limit as h tends to zero, meaning that it considers the behavior of f for all small values of h and extracts a consistent value for the case when h equals zero:
Geometrically, the derivative is the slope of the tangent line to the graph of f at a. The tangent line is a limit of secant lines just as the derivative is a limit of difference quotients. For this reason, the derivative is sometimes called the slope of the function f.
Here is a particular example, the derivative of the squaring function at the input 3. Let f(x) = x2 be the squaring function.
2. Computing Derivatives
We will investigate how the limit definition of the derivative
leads to interesting patterns and rules that enable us to quickly find a formula for f′(x) based on the formula for f(x) without using the limit definition directly. For example, we already know that if f(x) = x, then it follows that f′(x) = 1. While we could use the limit definition of the derivative to confirm this, we know it to be true because f(x) is a linear function with slope 1 at every value of x . One of our goals is to be able to take standard functions, say ones such as g(x) = 4x7 - sin(x) + 3ex, and, based on the algebraic form of the function, be able to apply shortcuts to almost immediately determine the formula for g'(x).
Activity 2.1
Functions of the form f(x) = xn, where n = 1,2,3,..., are often called power functions.
Solution:
b) Use the limit definition of the derivative to find f'(x) for f(x) = x3.
Solution: f'(x) = 5x4 & f'(x) = 13x12
Solution:
c) Use the limit definition of the derivative to find f'(x) for f(x) = x4 . (Hint:(a+b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4. See Binomial theorem for expansion of powers of a binomial. Apply this rule to (x+h)4 within the limit definition.)
Solution:
d) Based on your work in (a), (b), and (c), what do you conjecture is the derivative of f(x) = x5 ? Of f(x) = x13 ?
Solution: f'(x) = 5x4 & f'(x) = 13x12
e) Conjecture a formula for the derivative of f(x) = xn that holds for any positive integer n. That is, given f(x) = xn where n is a positive integer, what do you think is the formula for f'(x) ?
Solution: f'(x) = nxn-1
2.1 Constant, Power, and Exponential Functions
For instance, this rule tells us that if f(x) = 2x, then f'(x) = 2x ln(2). Similarly, for p(t) = 10t, p'(t) = 10t ln(10). It is especially important to note that when a = e, where e is the base of the natural logarithm function, we have that:
d/dx [ex] = ex ln(e) = ex since ln(e) = 1 . This is an extremely important property of the function ex : its derivative function is itself!
Note carefully the distinction between power functions and exponential functions: in power functions, the variable is in the base, as in x2, while in exponential functions, the variable is in the power, as in 2x . As we can see from the rules, this makes a big difference in the form of the derivative.
Activity 2.2
Use the three rules above to determine the derivative of each of the following functions. Foreach, state your answer using full and proper notation, labeling the derivative with its name. For example, if you are given a function h(z), you should write “h'(z) =” or “dh/dz=” as part of your response:(a) f(t) =π
- Solution: f'(t) = 0
(b) g(z) = 7z
- Solution: g'(z) = 7z ln(7)
(c) h(w) = w3/4
- Solution: h'(w) = 3/4 w-1/4
(d) p(x) = 31/2
- Solution: p'(x) = 0
(e) r(t) = (√ 2 )t
- Solution: r'(t) = (√ 2 )t ln(√ 2 )
(f) d/dq [q-1]
- Solution: d/dq [q-1] = -q-2
(g) m(t) = 1/t3
- Solution: m'(t) = -3 t-4
Continue: Derivatives of Constant Multiples and Sums of Functions
REFERENCES
https://en.wikipedia.org/?title=Calculus
Boelkins, M. (2012). http://faculty.gvsu.edu/boelkinm/
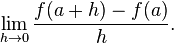
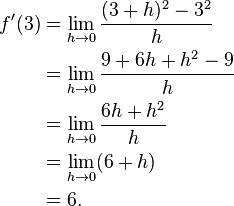






No comments:
Post a Comment